คณิตศาสตร์

วันจันทร์ที่ 17 กุมภาพันธ์ พ.ศ. 2557

ฟังก์ชันตรีโกณมิติ คือ ฟังก์ชันของมุม ซึ่งมีความสำคัญในการศึกษารูปสามเหลี่ยมและปรากฏการณ์ในลักษณะเป็นคาบ ฟังก์ชันอาจนิยามด้วยอัตราส่วนของด้าน 2 ด้านของรูปสามเหลี่ยมมุมฉาก หรืออัตราส่วนของพิกัดของจุดบนวงกลมหนึ่งหน่วย หรือนิยามในรูปทั่วไปเช่น อนุกรมอนันต์ หรือสมการเชิงอนุพันธ์ รูปสามเหลี่ยมที่นำมาใช้จะอยู่ในระนาบแบบยุคลิด ดังนั้น ผลรวมของมุมทุกมุมจึงเท่ากับ 180° เสมอ อ่านต่อ

ฟังก์ชัน	ตัวย่อ	ความสัมพันธ์
ไซน์ (Sine)	sin	$\sin \theta =\cos \left({\frac {\pi }{2}}-\theta \right)\,$
โคไซน์ (Cosine)	cos	$\cos \theta =\sin \left({\frac {\pi }{2}}-\theta \right)\,$
แทนเจนต์ (Tangent)	tan (หรือ tg)	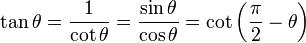$\tan \theta ={\frac {1}{\cot \theta }}={\frac {\sin \theta }{\cos \theta }}=\cot \left({\frac {\pi }{2}}-\theta \right)\,$
โคแทนเจนต์ (Cotangent)	cot (หรือ ctg หรือ ctn)	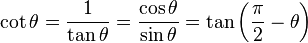$\cot \theta ={\frac {1}{\tan \theta }}={\frac {\cos \theta }{\sin \theta }}=\tan \left({\frac {\pi }{2}}-\theta \right)\,$
ซีแคนต์ (Secant)	sec	$\sec \theta ={\frac {1}{\cos \theta }}=\csc \left({\frac {\pi }{2}}-\theta \right)\,$
โคซีแคนต์ (Cosecant)	csc (หรือ cosec)	$\csc \theta ={\frac {1}{\sin \theta }}=\sec \left({\frac {\pi }{2}}-\theta \right)\,$